Terminal objects and products(17)
Terminal object(1)
terminal object in a category \(\mathcal{C}\)
An object z is terminal if, for each object c there exists a unique morphism \(c \xrightarrow{!} z\)
We say terminal objects have a universal property
Linked by
Product(1)
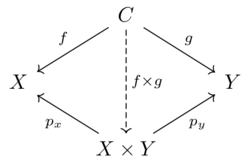
Given two objects \(X,Y \in \mathcal{C}\), the product \(X \times Y\)
This is another object in \(\mathcal{C}\) with morphisms \(X \xleftarrow{p_x}X\times Y\xrightarrow{p_y}Y\)
This should satisfy the property that there exists a unique morphism making the following diagram commute for any other object C and morphisms \(X \xleftarrow{f}C\xrightarrow{g}Y\)
Linked by
Terminal in Set(1)
In Set, any set with exactly one element is a terminal object. For an arbitrary other set, we have no choice but to send everything to that one object when specifying a function.
Product in Set(1)
In Set, the categorical product of two sets is our usual cartesian product.
The projections are \(x \xrightarrow{p_x}(x,y)\xrightarrow{p_y}y\)
The unique morphism from some \(X \xleftarrow{f} C \xrightarrow{g} Y\), the unique map \(C \xrightarrow{!}X \times Y\) is given by \((f\times g)(c):=(f(c),g(c))\).
Product in Cat(1)
The product of two categories \(\mathcal{C}\times \mathcal{D}\) may be given as follows:
\(Ob(C\times D)\) are the pairs \((c,d)\) where c is an object of \(\mathcal{C}\) and d is an object of \(\mathcal{D}\).
Morphisms are pairs \((c,d)\xrightarrow{(f,g)}(c',d')\) where \(c \xrightarrow{f}c'\) is a morphism in \(\mathcal{C}\) and \(d \xrightarrow{g}d'\) is a morphism in \(\mathcal{D}\).
Composition is given by composing each entry in the pair separately.
Linked by
Terminal objects are isomorphic(2)
Proof(1)
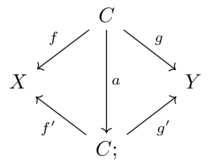
Suppose \(Z,Z'\) are both terminal objects. Therefore there exist unique maps \(Z \overset{a}{\underset{b}{\rightleftarrows}}Z'\)
Composing these we get \(Z \xrightarrow{a;b} Z\), but this is forced to be the identity map because there is only one morphism from \(Z\) to itself and we have to have an identity.
Therefore we can talk about ’the terminal object’ as if there were only one.
All terminal objects in a category \(\mathcal{C}\) are isomorphic
Exercise 3-81(2)
Let \(z \in P\) be an element of a preorder, and consider the corresponding category \(\mathcal{P}\). Show that z is a terminal object iff it is a top element in \(P\), i.e. \(\forall c \in P: c \leq z\)
Exercise 3-82(2)
Name a terminal object in the category Cat
Solution(1)
1 is terminal because a functor from any other category is forced to map all objects to 1 and all morphisms to its identity morphism.
Exercise 3-83(2)
Name a category which does not have a terminal object
Solution(1)
The category corresponding to the natural numbers has no terminal object (it would be an integer larger than all integers).
Exercise 3-88(2)
Let \(x,y \in P\) be elements of a preorder and \(\mathcal{P}\) be the corresponding category. Show that the product \(x \times y\) in \(\mathcal{P}\) agrees with their meet \(x \land y\) in \(P\).
Solution(1)
The uniqueness aspect of the product is not relevant since all morphisms are unique in a preorder category.
The product definition translates to an operation which takes a pair of objects in a preorder and gives us another object with the property that \(x \times y \leq x\) and \(x \times y \leq y\), and for any other b that also has this property we have \(b \leq x\times y\)
Considering the set \(A=\{x,y\}\), the conditions for \(x \times y\) matches the definition of \(\bigwedge A\) (grestest lower bound).
Exercise 3-90(2)
What are identity morphism in a product category \(\mathcal{C}\times \mathcal{D}\)?
Why is composition in a product category associative?
What is the product category \(1 \times 2\)?
What is the product category of two preorders?
Solution(1)
For object \((c,d)\), the identity morphism is \((id_c,id_d)\)
The operation was defined in terms of function composition which is associative.
It is isomorphic to just 2
The underlying set is the cartesian product, and \((a,b)\leq(a',b')\) iff \(a \leq a' \land b \leq b'\)